Shrifti kontuurid

BEZIER‘i kõver

Bezier`i kõvera autoriks on Prantuse insener Pierre Etienne Bézier (1910-1999). Bézier kasutas kõveraid Renault autokerede konstrueerimisel 1970-datel.

Suure resolutsiooniga jooniste/graafika ja teksti kujutamisel tagab parima tulemuse vektorgraafika. Vektorgraafika võimaldab esitada kujutisi nii suuremalt kui väiksemalt, säilitades kujutiste sujuvad piirjooned. Vektorite eeliseks on, et neid on lihtne salvestada – infomaht on võrreldes pikselpindadega väike. Kõik vektorid ja kuvamiseks vajalikud punktid on määratletud koordinaatide ja kindlate valemitega.

Bezier‘i kõver on väga levinud vektorite arvutamise meetod. Kõvera joonistamiseks kasutatakse kahte tüüpi punkte. Sõlmpunktid, mis asuvad alati vektoril ja kõveral mitte asuvad punktid, mille poole tavaliselt kõver kaardub. Et kujutada pikemat kõverat, on vaja ühendada mitu Bezier‘i kõverat. Tavaliselt tehakse siis ühe kõvera lõpppunkt teise alguspunktiks. Kurv läbib iga lõigu algus- ja lõpppunkti, mis teeb kõvera töötlemise lihtsaks ja meetodi enda populaarseks paljude vektorgraafika programmide töös.

Bezier‘i kõvera idee on küllaltki lihtne. Et kujutada pehmet ja sujuvat kõverat, ühendatakse esmalt sõlmpunktid vektoril mitte asuvate punktidega kurvi kaudsel trajektooril sirgega. Seejärel joonistatakse sirged, ühendamaks eelmiste sirgete keskpunkte ja seda korratakse seni, kuni joon on piisavalt sujuv. Kõvera joonistamine on kujutatud alltoodud joonisel.

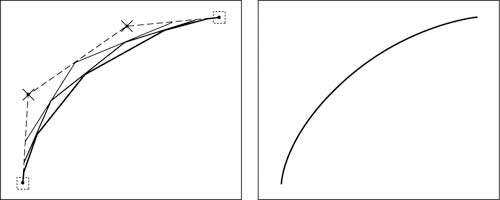
Joonis 6. Bezier‘i kõvera konstrueerimine ja kõver meile nähtuna. (Ruudud tähistavad kõvera joonel asuvaid sõlmpunkte, ristid kõveral mitte asuvaid punkte.)

Vektorkujutist on võimalik defineerida ja salvestada, kirjeldades ainult sõlmpunktide ja kõveral mitte asuvate punktide koordinaate.

Vektorite matemaatika

Vektorid koosnevad enamasti B-kõveratest, mis üksteisega ühendades moodustavad Bezier‘i kõvera. Iga B-kõver on defineeritud kolme piirjoone kontroll-punktiga, genereeritud vastavalt parameetritele, piirjoonte rasteriseerimiseks kasutatav võrrand on shrifti sisse programeeritud.

Kui kolm punkti kõveral on (Ax, Ay), (Bx, By) ja (Cx, Cy), siis:
px = (1-t)2.Ax + 2t(1-t).Bx + t2.Cx
py = (1-t)2.Ay + 2t(1-t).By + t2.Cy

Muutes parameetrit t 0-ist 1-ks genereerime kõik punktid p kõveral, mis on defineeritud parameetritega A, B ja C.
Visuaalselt, kõver jookseb kahe kõveral asuva kontrollpunkti A ja C vahel, kasutades joonel mitte asuvat kontrollpunkti B, et mõjutada joont kõverduma tema poole. Kõver väljub punktist A piki sirget AB ja siseneb punkti C piki sirget BC. (See teeb mugavaks ja lihtsaks nurga defineerimise ja kasutamise tangensi abil.)

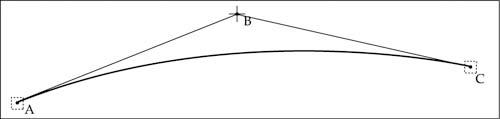
Joonis 7. Konstrueeritud kõver. (Ruudud tähistavad kõverate joonel asuvaid sõlmpunkte, ristid kõveral mitte asuvaid punkte.)

Joonisel olevad punktid A, B ja C vastavad eeltoodud võrrandile ja defineerivad ühe lõigu tähemärgi piirjoonest. Võimalik on, et mitmed kõveral mitte asuvad punktid on üksteise järjel, sellisel juhul tekib lõikumine tähe piirjoonega täpselt sirge keskel.

Tähemärgid on defineeritud nagu kontuuride seeriad, iga seeria koosneb kolmest või rohkemast punktist. Iga punkt on kas joonel asuv või väline punkt. On õimalik, et kontuur koosneb ainult kontuurivälistest punktidest.

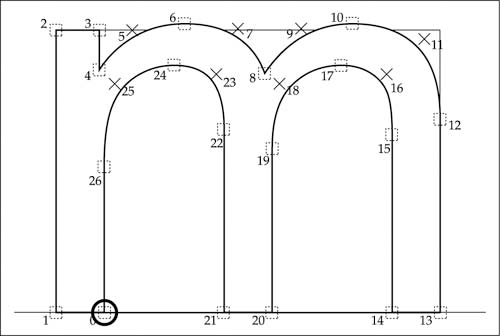
Joonis 8. Täht “m” shriftist Monotype Arial. Kontuuride seeriad: 4 - 6; 6-8 jne.

Täispinnad paremale

Hooletult tehtud shriftide probleemiks on sageli see, et kujundid lõikavad iseennast või kattuvad üksteisega, paljud tarkvaralised lahendused ei suuda sellisel juhul neid hallata, või teevad seda vigaselt. Korrektses shriftis on täispinnad defineeritud nii, et sõlmpunktid asuvad piirjoonel päripäeva. Täispindades välja lõigatud kujundid defineeritakse vastupäeva.

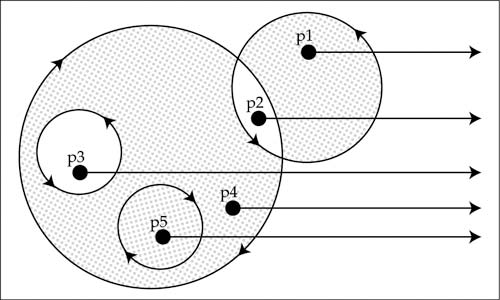
Joonis 9. Vastavalt sellele, kas piirjoon on päripäeva või vastupäeva, defineeritakse tema pind täispinnaks või auguks teises kujundis. Samuti saab skeemi vaadates küsida, kas näidatud punktid asuvad kujundi sees või väljas? Otsustamiseks kontrollitakse, kas punktil on pöörlemise suund või ei.

- Punktid p1 ja p4 asuvad ühe kindla kujundi sees, see annab neile mingi kindla suuna - kas siis päripäeva või vastupäeva, tähendab nad on kujundi sisesed punktid.
- Punkt p2 asub nii vastu kui päripäeva kujundi sees, seega liikumised liites saame suunaks null ja punkt on väline.
- Punktid p3 ja p5 illustreerivad seda, kui oluline on, et piirjoontele suund oleks korrektselt defineeritud. Punkt p3 puhul nullib piirjoonte vastastikune suund jällegi punkti suuna - tegemist on välise punktiga. Punktil p5 aga liituvad liikumised ja seega on punktil kindel suund ja ta on kujundi sisene punkt.

On olemas kolme liiki tähemärke:

- Lihtsad tähemärgid sisaldavad lihtsalt oma piirjooni.
- Kombineeritud tähemärgid viitavad teistele tähemärkidele, et kombineerida oma piirjooned mitme tähemärgi piirjoontest. Viidatud komponendid võivad olla lihtsad või samuti kombineeritud. Tavapäraseim kombineeritud tähemärk on näiteks rõhumärgiga täht.
- Null-kontuuriga tähemärk, nagu näiteks tühik, tähistab mingeid omadusi tekstis, aga ei oma trükitavat väljundit. Null-kontuuriga tähemärkidel, nagu kõigil tähemärkidel, on vasakpoolne joondus, aga nende parameetrid ei ole muudetavad nii nagu nad on muudetavad tavaliste tähemärkida puhul.

Materjalid Bezier`i kõvera kohta
___________________________
2-D Curve Generation - Darren Meyer, WPI CS Department - www.cs.wpi.edu
Bezier curves - Luc Devroye, School of Computer Science, McGill University - cgm.cs.mcgill.ca

Materjalid
___________________________
AAT Font Quality Specification - Apple Computer, Inc. - developer.apple.com/fonts
TrueType Outlines - TYPE chimérique - www.truetype.demon.co.uk
Converting Outlines to the TrueType Format - Apple Computer, Inc. - developer.apple.com/fonts

<< TAGASI